A Base Teórica
Desde tempos imemoriais o homem observou a natureza e percebeu que algumas proporções se manifestavam de maneira mais frequente que outras na natureza, e que as coisas onde essas proporções se manifestavam eram mais belas e atraentes. A mais notável destas proporções foi chamada de “medida áurea”, pois manifestava a perfeição da natureza tanto quanto o ouro.
Veja exemplos:
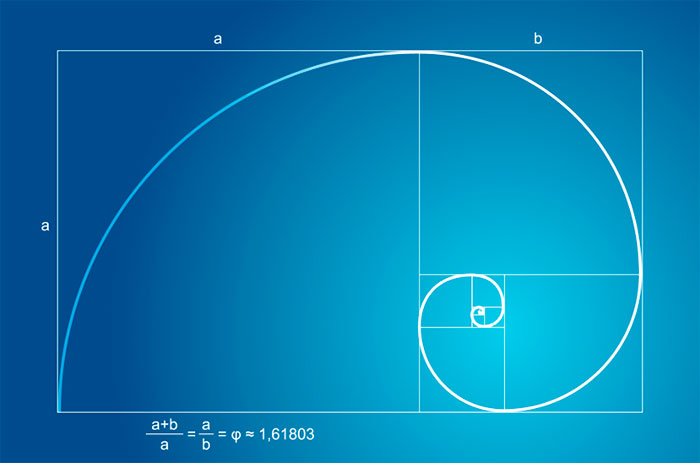
01 – A medida áurea é a proporção entre o lado vertical, ao qual se atribuiu um valor 1, e o lado horizontal, cujo valor é o número irracional 1,618…

02 – Tubarão – Os vários segmentos do corpo do animal estão em proporção uns com os outros.
03 – Borboleta.
A mesma proporção pode ser observada nas asas de uma borboleta.
Vários monumentos da antiguidade foram erigidos baseados nesta medida, entre eles podemos destacar a Pirâmide de Quéops e o Partenon. Esta proporção foi utilizada pelos gregos para espelhar o corpo humano ideal, na relação entre a altura da cabeça e medida dos olhos ao queixo, na relação entre o comprimento do cotovelo à ponta dos dedos e o comprimento da mão, e várias outras proporções corporais.
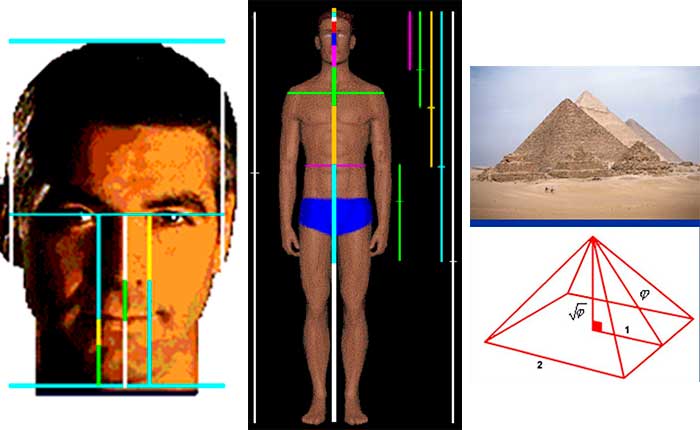
Figuras 04, 05 e 06 – A medida áurea pode ser aplicada ao rosto humano, evidenciando a proporção entre seus diversos traços. O mesmo se aplica em relação ao corpo humano como um todo, e também à representação esquemática da pirâmide de Quéops. Se metade da largura da base for igual a 1, o valor da altura será de 1,618…

07 – Representação frontal do Partenon, templo dedicado à deusa Atena na época de ouro da cultura grega. Observe que toda a construção obedece a proporções rigorosas, como nas relações largura total x altura total; altura total x altura da área acima das colunas; altura da área acima das colunas x altura do intervalo entre as colunas o frontão (parte triangular) etc.
No século IV a.C., Pitágoras viaja ao Egito, à Babilônia e a Creta, entrando em contato com as escolas locais de mistérios. Depois funda no sul da Itália a sua própria escola de mistérios, nos moldes egípcios, baseada nos seguintes princípios:
1) No seu nível mais profundo, a natureza da realidade é matemática.
2) A filosofia pode ser usada para a purificação espiritual.
3) A alma pode se unir ao divino.
4) Alguns símbolos têm um significado místico.
5) Os Irmãos da Ordem devem observar total lealdade e sigilo.
A escola Pitagórica é a mais antiga escola de mistérios de que temos registros mais detalhados, e a preocupação de Pitágoras com a matemática era tanta que mandou entalhar na porta da escola a frase: “Aquele que não sabe matemática, jamais entre aqui.” Seus membros eram chamados de “mathematikoi”, eram vegetarianos e não tinham posses pessoais.
Os Pitagóricos foram os descobridores dos números irracionais, entre eles o pi. Pitágoras se interessou profundamente pela medida áurea, e percebeu que em um pentágono regular onde cada lado valesse 1, a relação entre este lado e uma reta que unisse dois cantos não consecutivos teria esta proporção. Pitágoras chamou este comprimento de phi.
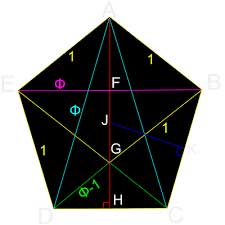
08 – Pentágono
Observe que, no pentágono, se atribuirmos a cada lado um valor 1, as retas que unem dois lados não consecutivos (formando uma estrela de cinco pontas) têm valor igual a phi. Os segmentos que vão de cada aresta do pentágono até a interseção destas retas têm valor igual a 1/phi.
Um século depois, Platão enunciou as 7 Nobres Artes Liberais, o conjunto de conhecimentos que todo homem livre deveria ter para que fosse considerado como tal. Esta definição de Platão foi posteriormente divulgada por Aristóteles e usada como base para toda a estrutura universitária do século XII ao XVII. Estas 7 Artes se dividiam em dois grupos: trívia, de onde vem a palavra trivial, que englobava a dialética, a gramática e a retórica, e quadrívia (ou quadrivium), o conhecimento mais aprofundado, que englobava aritmética, geometria, astrologia e música.
Desta maneira, Platão estabeleceu uma conexão incontestável entre estes quatro assuntos, e foi um mestre em todos eles. Seus estudo tanto de música, com a teoria da música das esferas, quanto de geometria e matemática foram a base para o desenvolvimento de muitas teorias astrológicas.
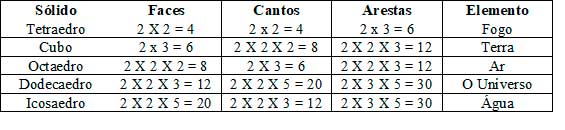
Platão considerava os números 2, 3 e 5 de vital importância, pois, além de serem números primos, tudo na natureza se manifestava segundo estes princípios. Através do estudo destes números aplicados à geometria chegou aos 5 primeiros sólidos platônicos, que associou aos elementos da natureza.
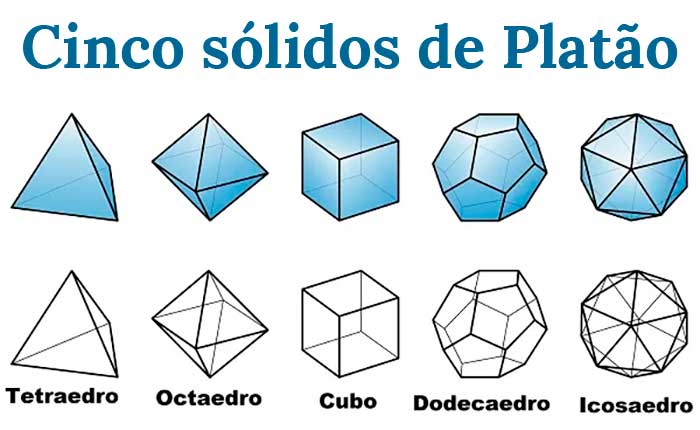
09 – Os cinco primeiros sólidos platônicos. Da esquerda para a direita: tetraedro (quatro faces), octaedro (oito faces), cubo (seis faces), dodecaedro (12 faces) e icosaedro (20 faces).
Estes sólidos teriam importância fundamental nas teorias de Kepler, mas chegaremos lá oportunamente.
No século II a.C. o grande matemático Euclides é o primeiro a calcular o valor de phi. Euclides percebeu o seguinte:
A———————B———-C
Se tivermos uma reta AC e a reta AB for proporcional a AC na medida áurea, a equação que rege estas proporções é:
AC/BC = BC/AB = Phi
Aplicando valores a esta relação, Euclides chegou ào valor de Phi:
Phi= (raiz quadrada de 5 + 1)/2 = 1,61803398874989……
Além disto, notou outras interessantes correlações matemáticas:
Phi ao quadrado = 2,61804…
portanto
Phi ao quadrado = Phi + 1
1/Phi = 0, 61804…
portanto
1/Phi = Phi – 1
Phi = (5 elevado a 0,5) X 0,5 + 0,5
Além de tudo isto, o número Phi se inseria em todas as proporções do pentágono e do pentagrama regulares, estando associando ao ângulo de 72º, além de ser a medida encontrada se traçarmos um arco com um compasso ligando o centro de um dos lados de um quadrado a um dos cantos opostos.
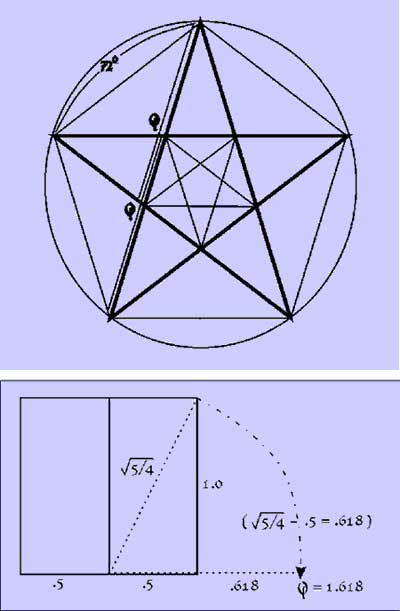
10 – Acima o pentagrama, relacionado ao ângulo de 72 graus; abaixo o quadrado com a representação do arco citado no parágrafo anterior.
Nada mais foi acrescentado a este conhecimento até o século XII, quando o matemático italiano Leonardo Fibonacci decidiu resolver um problema que intrigava os matemáticos da época: Se um casal de coelhos pode dar a luz a outro casal de coelhos por mês, e os coelhos recém nascidos demorarem um mês para ficar adultos, quantos casais de coelhos adultos teremos após um período de “n” meses? Fibonnacci chegou à seguinte tabela:
| Mês | Casais Adultos | Casais Jovens |
| 1 | 1 | – |
| 2 | 1 | 1 |
| 3 | 2 | 1 |
| 4 | 3 | 2 |
| 5 | 5 | 3 |
Fibonacci percebeu que a resposta sempre era a soma dos dois meses anteriores, e com isto construiu a famosa “Série de Fibonacci”: 1,1,2,3,5,8,13,21,34,55,89… Também percebeu que esta série se manifestava a toda hora na natureza, no desenvolvimento dos galhos de uma árvore, nos círculos concêntricos de pétalas de uma rosa, nas sementes de uma pinha.

11 – A “Série de Fibonacci” manifestada no crescimento dos galhos de uma árvore… 12 – Na disposição das sementes da pinha… 13 – E nas pétalas da rosa, demonstrando a presença de proporções geométricas nos sistemas biológicos.
Estudando mais profundamente, percebeu que a razão entre os números de sua série, multiplicados pelo Lá básico de 440Hz e temperados, produzia todas as notas musicais:
| Razão | Frequência Calculada | Frequência Temperada | Nota |
| 1/1 | 440 | 440 | Lá |
| 2/1 | 880 | 880 | Lá |
| 2/3 | 293,33 | 293,66 | Ré |
| 2/5 | 176 | 174,62 | Fá |
| 3/2 | 660 | 659,26 | Mi |
| 3/5 | 264 | 261,63 | Dó |
| 3/8 | 165 | 164,82 | Mi |
| 5/2 | 1.100 | 1.108,72 | Dó# |
| 5/3 | 733,33 | 740 | Fá# |
| 5/8 | 275 | 277,18 | Dó# |
| 8/3 | 1.173,33 | 1.174,64 | Ré |
| 8/5 | 704 | 698,46 | Fá |
Ainda fazendo experiências com a razão entre os números de sua série, Fibonacci percebeu que a razão entre um número e o número anterior tendia sempre a Phi, ligando definitivamente sua série com a Medida Áurea.
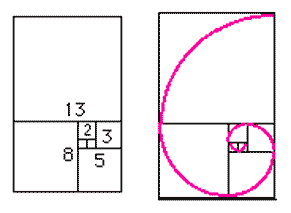
14 – Representação esquemática da “Série de Fibonacci”: a área de cada quadrilátero expressa cada número da série. 15 – O mesmo desenho esquemático, servindo agora como base para o traçado de uma espiral, forma presente desde o DNA até a organização das galáxias.
No século XVII surge Kepler, que se interessa pelas teorias de Platão sobre a música das esferas, pesquisa o assunto e escreve o livro “A Harmonia dos Mundos”. Neste livro, Kepler declara: “Quando Deus criou o universo e regulamentou a ordem do cosmos, tinha em vista os cinco corpos regulares da geometria, como conhecemos desde os dias de Pitágoras e Platão.”
Segundo Kepler, as órbitas médias dos planetas em relação ao Sol estariam colocadas na mesma proporção que os sólidos platônicos circunscritos uns dentro dos outros.
Kepler percebeu todas estas correlações matemáticas e foi o criador do aspecto de 72 graus, o chamado “quintil” e de seu irmão, o aspecto de 144 graus, o “biquintil”, relacionando estes aspectos à perfeição e à criatividade da natureza.
Após a descoberta de Plutão em 1930, pudemos mais uma vez ver a força e a importância do Phi na maneira com que a natureza se manifesta, pois se somarmos a distância média relativa dos planetas e Ceres ao Sol, considerando a distância Mercúrio – Sol como 1, teremos o valor 10 Phi.
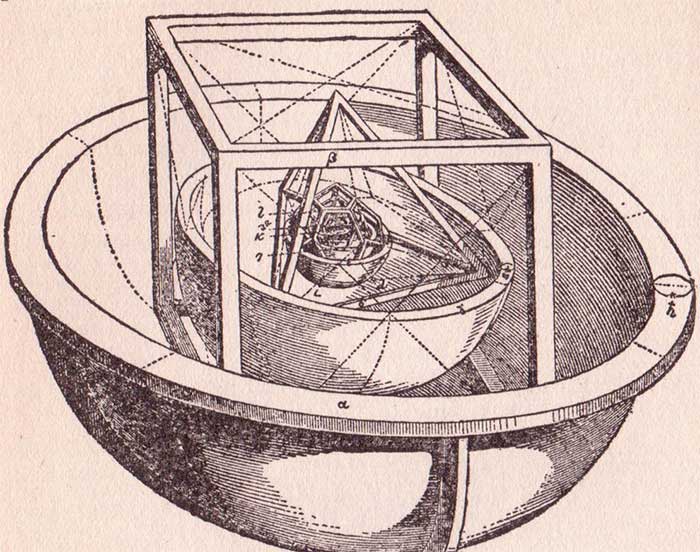
16 – Reprodução de ilustração de obra de Kepler, em que as órbitas dos planetas são associadas aos cinco sólidos de Platão.
Além disto a genética determinou que a proporção da hélice dupla do DNA apresenta a medida áurea e um corte transversal de uma de suas hélices apresenta o formato do decágono, dois pentágonos superpostos, um para cima e outro para baixo.
Recentemente o astrólogo russo Sergey Smeliakov fez uma projeção da série de Fibonacci à história da China e ao calendário Maia, provando desta maneira como funciona a aceleração do tempo.



É muito interessante, mas terei que estudar muito para conseguir compreender tudo.
Mas isso, me fascina.
Genial esse artigo. Ainda por cima lembrei quando criança assistia um desenho do Professor Pardal e os sobrinhos, ele dando uma aula, enlouquecido sobre a proporção áurea. Adorei!
Faz sentido, Joice, Pá Falcão, com todo seu conhecimento técnico e acadêmico, era mesmo uma espécie de “Professora Pardal” do meio astrológico. Aguarde a segunda parte, que é ainda mais interessante!